非厄米系统能够展现厄米系统所没有的奇异拓扑特征。非厄米性使得零维的点状拓扑缺陷扩展为一维的环状物体，称为外尔奇异环（WER），沿着该环系统的本征能和本征态都发生简并。WER可看作一个环状的磁单极，其所发出的虚拟磁场的强度相当于参数空间中的贝里曲率。这样的一维人工磁单极的拓扑效应可由陈数表征，其定义为参数空间中穿过包围该磁单极的二维流形的贝里磁通量。WER及其拓扑相变是非厄米系统区别于厄米系统的一个显著特征，但尚未在真正的量子系统中得到实现。

最近，量子信息与量子光学实验室郑仕标课题组基于电路量子电动力学结构，实现了这种奇异的拓扑物体，并观察到了相应的拓扑相变。研究人员利用一个超导比特及其读取腔合成了一个非厄米系统，其非厄米效应体现在读取腔的耗散。超导比特和读取腔通过参量调制发生边带耦合，其耦合强度和失谐量作为两个控制参数，由参量调制的幅度和频率控制。研究人员通过观测系统的态演化，并对结果进行后选择，提取了非厄米哈密顿的本征态，在此基础上得到了贝里曲率和陈数。研究人员通过缩小流形的尺寸，使得其由包围WER变成被WER环绕，观测到了陈数由1变成0的拓扑相变。此外，研究人员测量了沿着不同环路的贝里相位，并通过缩小环路的尺寸，使得其由环绕WER变成不环绕WER，观测到了贝里相位的突变。

团队工作将WER的实验研究从经典拓展到全量子领域，并首次观测到了非厄米系统的陈数。研究结果发表于Science Bulletin 70, 2446 (2025)，该刊物为国内顶级的综合性学术期刊，最新影响因子21.1。

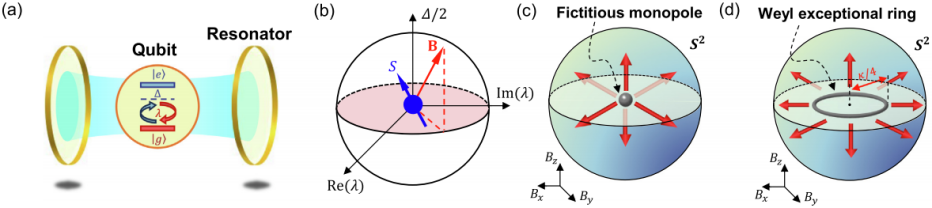
外尔奇异环的构建示意图